When I was in secondary school, I was taught the ever familiar c² = a² + b² for the right triangle. This is the well known Pythagorean Theorem [1]

The Pythagorean Theorem is a super easy way to compute lengths of many objects because at lot of objects can be simplified into right triangles; unfortunately, the Pythagorean Theorem only works for right triangles. To demonstrate the Pythagorean Theorem, I use an example.

Suppose for a minute that you managed a large nature center called Blue Mountain Arboretum as seen in Figure#1 below:

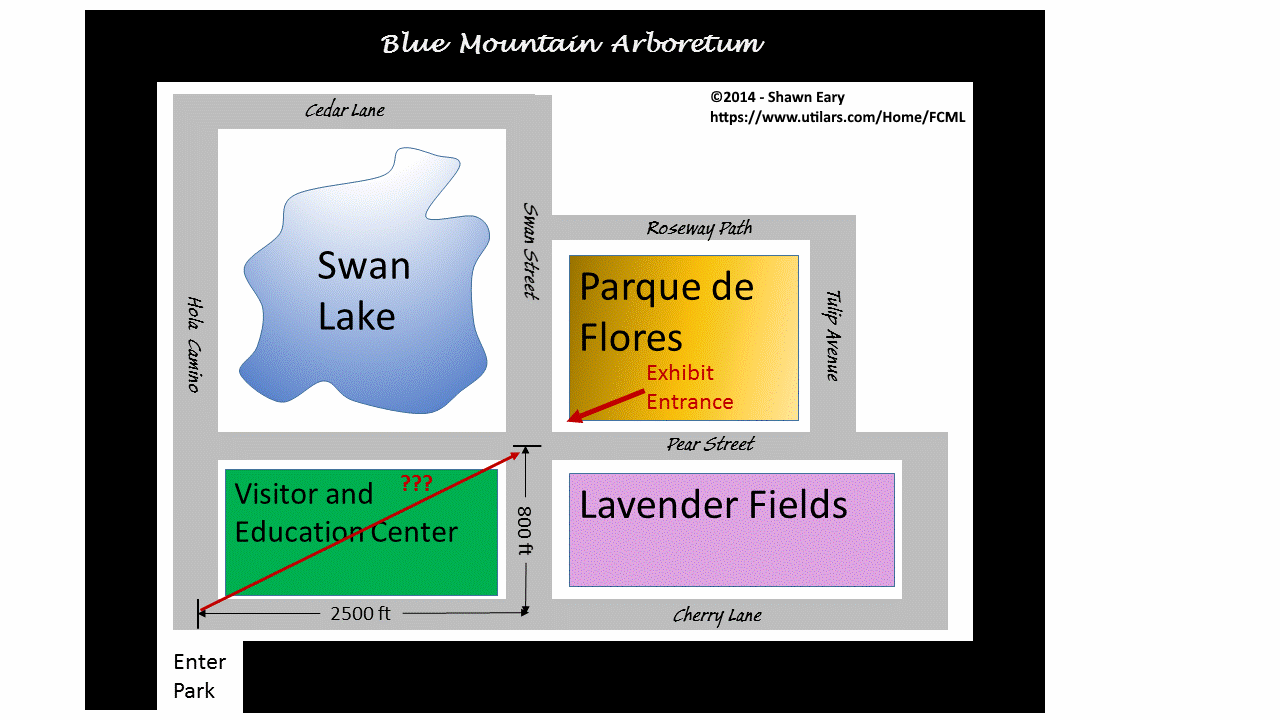
Further suppose that your patrons lost interest in the Visitor and Education Center shown in Figure#1 and instead became more interested in the new Parque de Flores exhibit. After receiving several complaints from patrons about how long and boring the walk around the Visitor Center was, you consider commissioning some engineers to build a path through the Visitor Center from the intersection of Hola Camino and Cherry Lane to the intersection of Swan Street and Pear Street.

Presently, your patrons have to travel approximately 2500 ft + 800 ft for a total of 3300 ft to get from the park entrance to the intersection of Swan Street and Pear Street, but you are wondering if allowing them to cut diagonally through the center would save them much walking distance so you decide to use the Pythagorean Theorem.

The Pythagorean Theorem works for you because Swan Street and Cherry Lane form a right angle and the path we want across the visitor center is a hypotenuse opposite that said right angle. Now, if you use the Pythagorean Theorem and do the math, your work might look something like this:

c² = a² + b²
c² = 2500² + 800²
c² = 6250000 + 640000
c² = 6890000
c² = 689 * 10000
$c=\sqrt{689}*\sqrt{10000}$
$c=\sqrt{689}*100$
$c=100*\sqrt{689}$
$c\approx 2624.88095$

Which is significantly shorter than the 3300 ft the patrons would have to walk if they didn't have a path to cut directly through the middle of the Visitor/Education Center. Given this information, you decide that it might be worth the cost to build that bridge or tunnel to cut through.

Again, the problem with this approach is that the Pythagorean Theorem only works on triangles with right angles. If the roads where slanted as in Figure#2, you would not be able to use the Pythagorean Theorem.

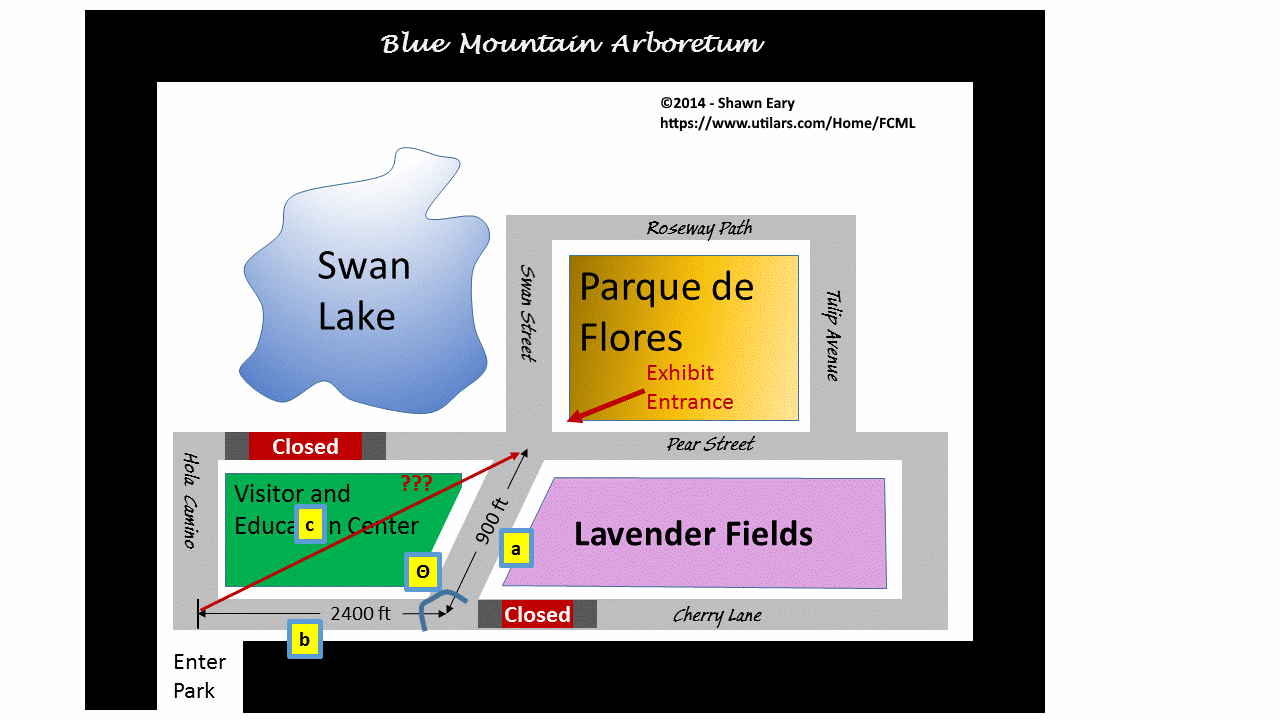
To overcome this, you could *try* to find a right triangle that has the edge "c" as a hypotenuse; unfortunately, that proves to be a bit difficult due to the lack of roads and closings on Pear Street and Cherry Lane. Instead of trying to find a such a right triangle, it might be easier to go ahead and use the Law of Cosines which according to [2] says:
c² = a² + b² - 2ab cos Θ

This doesn't look too much different than the Pythagorean Theorem except for the weird "- 2ab cos Θ" term on the end which we will get to later.

So you already know that the part of Cherry Lane from Hola Camino to Swan Street is 2400 ft (edge b) because it was measured by tape and you also already know that the part of Swan Street from Cherry Lane to Pear Street is 900 ft (edge a) from the same technique. The only thing you don't know is the angle that Cherry Lane and Swan Street make (Angle Θ) when they interect. This is easy to get though.

To find the Angle Θ, you send a worker out with her super duper survey compass to the intersection of Swan Street and Cherry Lane and find out that Cherry lane points 243 degrees going west and that Swan Street points 3 degrees going North. Since 360 is directly North, your worker finds the angle spread by subracting 243 from 360 and then adding the remaining 3 degrees. This would give us an equation similar to Θ = (360 - 243) + 3 = 120 degress which is (120 * π) / 180 radians.

From the law of cosines, you can then compute the distance as follows:
$c^2={2400}^2+{900}^2-2*2400*900cos\left(\frac{120\pi }{\mathrm{180}}\right)$
$c^2=5760000+810000-4320000cos\left(\frac{120\pi }{\mathrm{180}}\right)$
$c^2=6570000-4320000cos\left(\frac{12\pi }{\mathrm{18}}\right)$
$c^2=6570000-4320000cos\left(\frac{2\pi }{3}\right)$
Then according to [3] cos(2π/3) is -1/2 so you have:
$c^2=6570000-(4320000*\frac{-1}{2})$
which is
$c^2=6570000-\left(-2160000\right)$
$c^2=6570000+2160000$
$c^2=8730000$
$c^2=873*10000$
$c^2=97*9*10000$
$c=\sqrt{97}*\sqrt{9}*\sqrt{10000}$
$c=\sqrt{97}*3*100$
$c=\sqrt{97}*300$
$c=300\sqrt{97}$
$c\approx 2954.657341$

This is longer than the longest edge of 2400ft but shorter than the total walking distance of 2400+900=3300ft. So you can save your patrons some walking distance by cutting across the Visitor Center even in the scenario where the roads are angled.

So we have seen how the law of cosines works for angles other than 90 degrees or π/2 radians, but does is it really work just like the Pythagorean Theorem? According to [4] it does. Because if you substitute 90 degrees which equals π/2 radians into the formula, you get:
c² = a² + b² - 2ab cos (π/2)
c² = a² + b² - 2ab (0)
c² = a² + b² - (0)
c² = a² + b² - (0)
which is the Pythagorean Theorem.

As another extreme example, consider the situation where the angle is 180 degrees or π radians. Then we have a straight line with both edges comming right after each other. This looks like the Figure#3

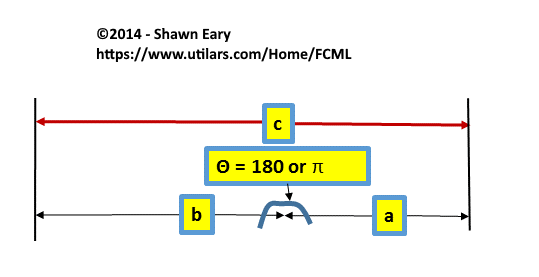
Then we have:
c² = a² + b² - 2ab cos (π)
c² = a² + b² - 2ab (-1)
c² = a² + b² + 2ab
c² = a² + 2ab + b²
c² = (a+b)(a+b)
c = a+b
which is intuitive by the picture. When Θ = 180 or π, then the Law of Cosines shows that the hypotenuse of the "triangle" is simply the sum of the lengths of the two sides a and b.

On the other extreme, consider angles less than 90 degrees or π/2. What happens to the triangle as Θ approaches 0. As Θ gets smaller and smaller, the triangle starts looking like a line again, but this time instead of segments a and b extending each other they seem to overlap each other. Leaving c to be the difference between b and a as in Figure 4:

So you can see that while we didn't prove the law of cosines, we did show (with help from references) that it is an extension of the Pythagorean Theorem and that it works in the special cases where Θ = π and Θ = 0. It is useful to have this law of cosines available in your toolbox for instances when the Pythagorean Theorem won't work. Also, since the Pythagorean Theorem is just a special case of the Law of Cosines, there is no longer any need to remember the Pythagorean Theorem itself (if you could ever forget it). Personally, I will just keep the Law of Cosines in my head moving forward...

Bibliography

[1] - Various.
Pythagorean Theorem
Wikipedia. [Online] August 16, 2014.
[Cited: August 27, 2014.]
https://en.wikipedia.org/wiki/Pythagorean_theorem

[2] - R. E. Larson, R. P. Hostetler and B. H. Edwards,
"Right Inside Cover," in Calculus - Fourth Edition,
D.C. Heath, 1990.
0-669-16406-2

[3] - Belk Jim.
Unit Circle Angles (SVG Diagram)
Wikipedia. [Online] November 14, 2010.
[Cited: September 23, 2014.]
https://en.wikipedia.org/wiki/Unit_circle#mediaviewer/File:Unit_circle_angles_color.svg

[4] - Various.
Law of Cosines
Wikipedia. [Online] September 4, 2014.
[Cited: September 23, 2014.]
https://en.wikipedia.org/wiki/Law_of_cosines

©2014 - Shawn Eary
This post is copyright (where allowable) by Shawn Eary and is released under the Free Christian Media Licence (FCML). Content from authors other than Shawn Eary maintain the copyright and licnese rules that were imposed by the original authors.